I momenti e le grandezze della fotogrammetria.
La pratica fotogrammetrica comporta la risoluzione di un problema analitico,
che è quello di relazionare lo spazio oggetto (X,Y,Z) tridimensionale con
lo spazio immagine (ξ,η) bidimensionale, e questo deve avvenire in modo
univoco, così da poter far corrispondere punti discreti, opportunamente
scelti, nei due sistemi. In fotogrammetria si individuano pertanto tre
tipi di grandezze.
- Le coordinate nelle tre dimensioni dello spazio oggetto (X,Y,Z).
- Le coordinate piane dello spazio immagine (ξ,η).
- I valori dei parametri della trasformazione Γ.
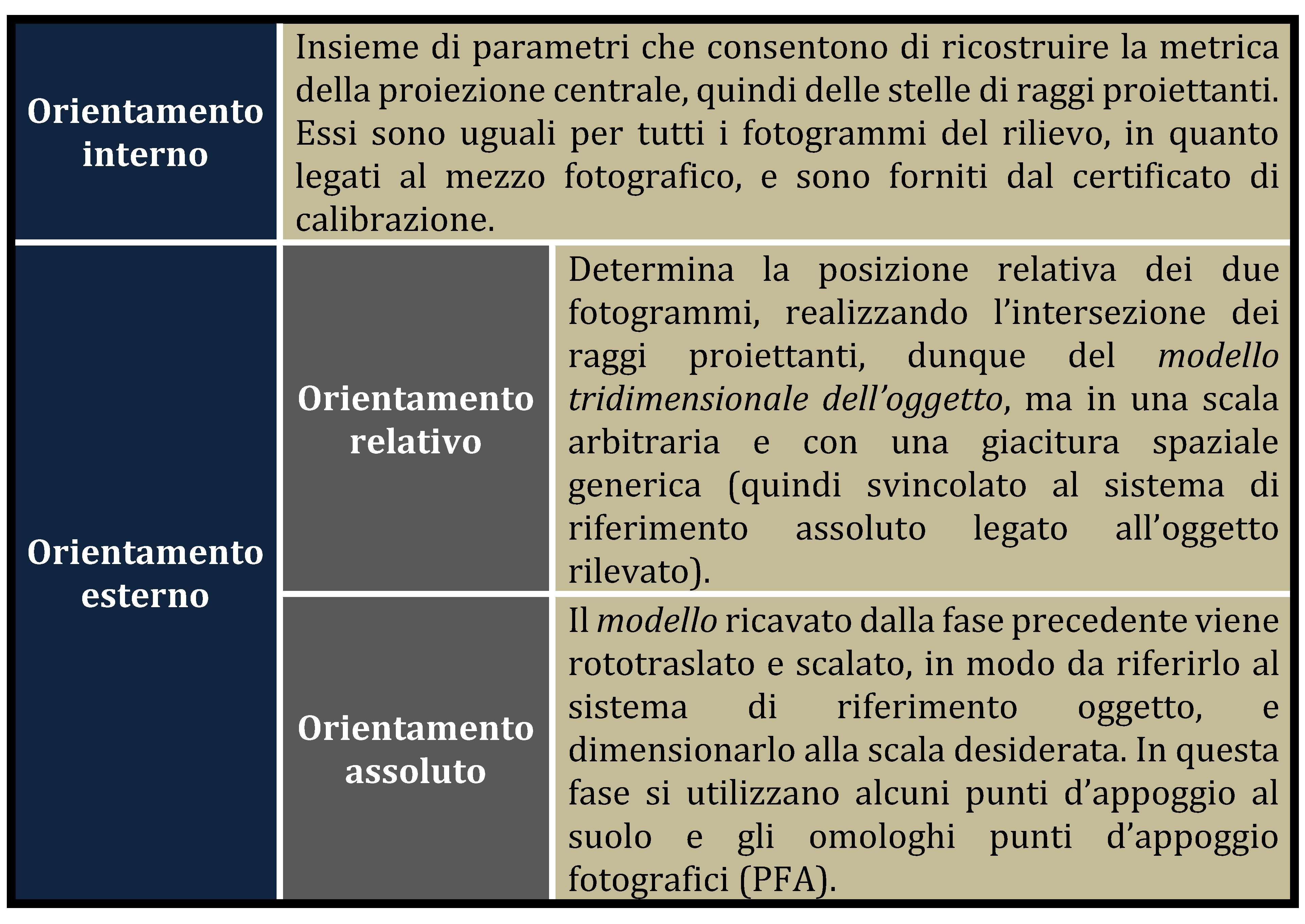
I parametri di trasformazione o di orientamento Γ, governano i rapporti
tra lo spazio oggetto e quello immagine, ed essi esprimono le caratteristiche
del mezzo fotografico e il suo posizionamento tra i due tipi di spazi.
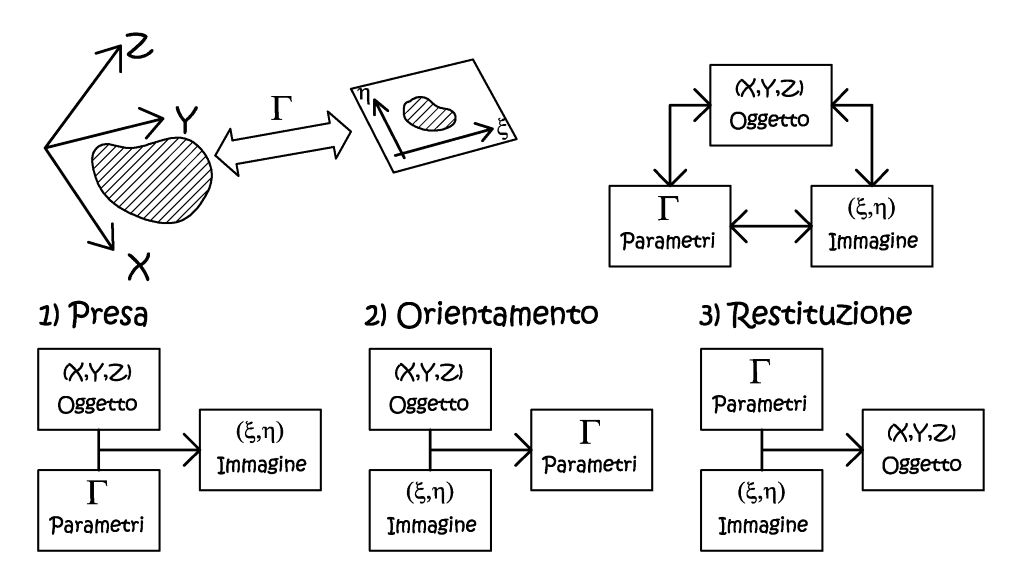
Fig. 2.29 – Le grandezze e le fasi del rilievo fotogrammetrico.
Nella fase di presa si acquisiscono i dati primari, dei quali abbiamo
già scritto, in questa fase sono noti due gruppi di grandezze: l’oggetto
del rilievo e il mezzo fotografico, quindi i parametri della trasformazione,
restano ignote le coordinate immagine nello spazio bidimensionale. Nella
fase di orientamento oltre ai parametri già noti del mezzo fotografico,
se ne deducono altri, che fissano la posizione relativa delle prese fra
loro, e la loro posizione assoluta, rispetto all’oggetto. Per far ciò abbiamo
la necessità di conoscere la relativa posizione di punti noti –punti d’appoggio-,
sia nello spazio oggetto, sia nello spazio immagine (PFA – punti fotografici
d’appoggio). Potremmo definire, in termini analitici, che questa fase corrisponda
alla calibrazione del modello matematico, e alla sua successiva validazione,
ad esempio, introducendo dei punti di controllo (check-points) usati esclusivamente
per valutarne il loro scarto quadratico medio (RMS). Nella tabella seguente
viene descritto l’usuale svolgimento della fase d’orientamento fotogrammetrico,
in particolare, si noti il passaggio intermedio alle coordinate modello,
in uso nell’epoca dei restitutori analitici/analogici: oggi, con le stazioni
fotogrammetriche digitali, tale passaggio rimane implicito, ed è fornito
direttamente in output dall’algoritmo di calcolo.
La metrica che governa la presa è quella della prospettiva centrale, dunque eseguire l’orientamento interno consiste nel conoscere e/o definire i parametri che consentono di ricostruirla su supporto fotografico. In altri termini si tratta di fissare la stella proiettiva (Fig. 2.30) del mezzo fotografico attraverso la conoscenza dei parametri riportati nella pagina seguente.

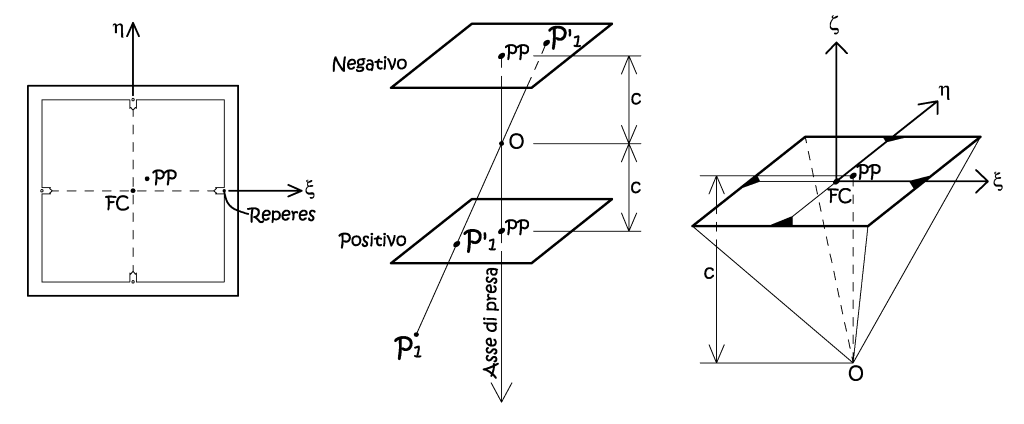
Fig. 2.30 – Schema dell’orientamento interno.
Il sistema di riferimento nello spazio immagine ha l’origine individuata dal centro fiduciale FC, fissato dall’intersezione dei segmenti congiungenti le marche fiduciali (reperes). Tra i parametri d’orientamento interno troviamo le coordinate immagine del punto principale PP, definito dal piede della perpendicolare, portata dal centro della prospettiva O, al piano dell’immagine medesima. Ciò unito alla conoscenza della distanza principale c, si può definire in modo univoco la configurazione spaziale della proiettività interna. Mentre l’orientamento esterno fissa la posizione e l’assetto della camera nel sistema di coordinate oggetto, quindi si devono conoscere le coordinate del punto di presa O, e gli angoli d’assetto della camera, denominati anche parametri di rollio.

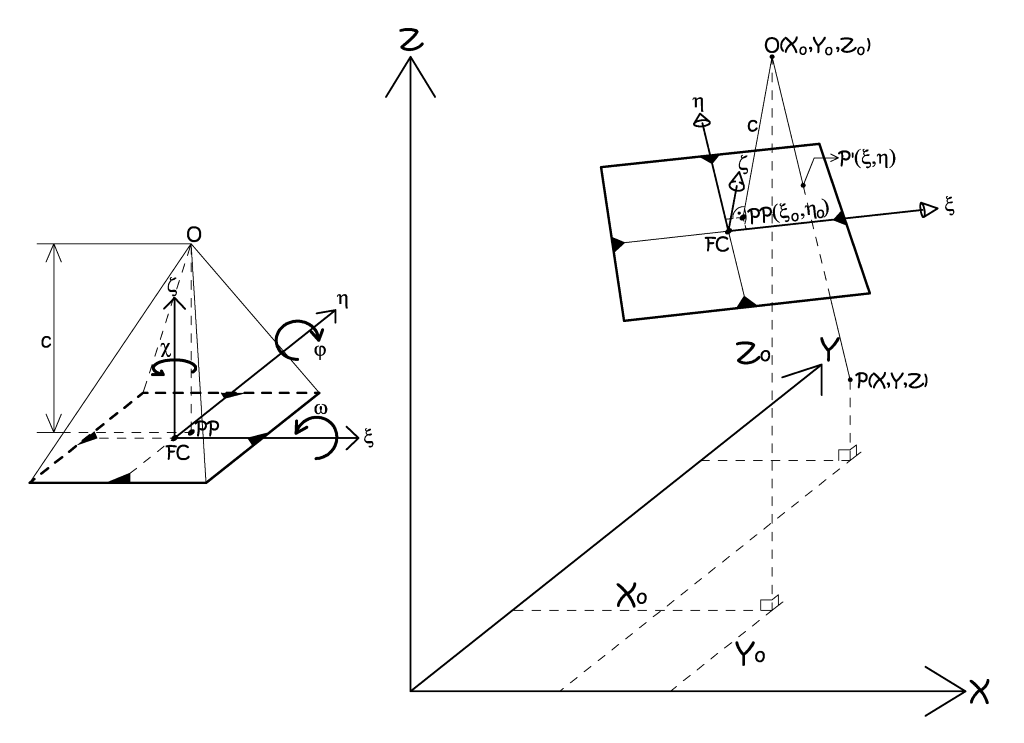
Fig. 2.31 – Schema dell’orientamento esterno.
La definizione della prospettiva centrale, rappresentata da un fotogramma, richiede in totale nove parametri; i tre parametri d’orientamento interno sono riportati nel certificato di calibrazione, o possono essere ricavati, per i vecchi voli, da procedure empiriche, mentre i sei parametri d’orientamento esterno possono essere ottenuti con metodi analitici, a partire dalla conoscenza di un numero discreto di punti d’appoggio fotografici (PFA).
L’ultima fase del processo fotogrammetrico è la restituzione, cioè l’insieme delle procedure codificate dai mezzi e dalla pratica, atte ad ottenere il passaggio dalle coordinate piane dello spazio immagine (ξ,η), alle coordinate corrispondenti dello spazio oggetto (X,Y,Z). In altri termini si procede alla ricostruzione tridimensionale degli oggetti rilevati, gli strumenti che permettono ciò si suddividono in tre categorie: gli analogici, gli analitici, i digitali. Dei primi due si è già scritto, nella storiografia, e dato che non vengono più utilizzati, non saranno oggetto di ulteriori approfondimenti, mentre i sistemi di restituzione digitali verranno descritti più avanti.
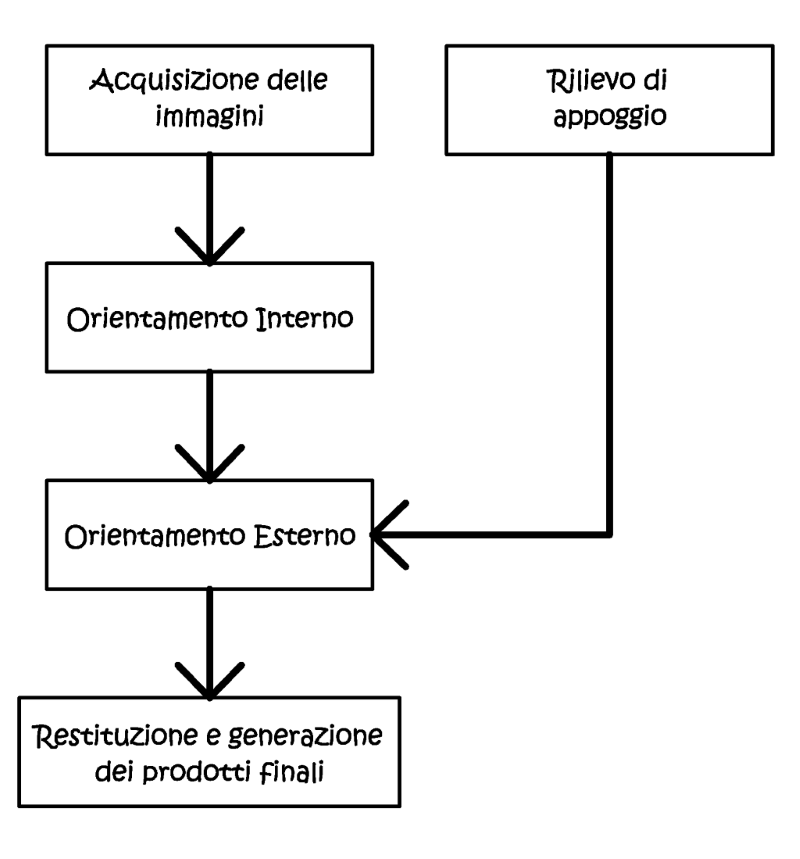
Fig. 2.32 – Il data processing del rilievo fotogrammetrico.
I fondamenti analitici della fotogrammetria.
Nell’ipotesi di una prospettiva centrale rigorosa, il punto oggetto, il centro di presa O e il punto immagine corrispondente, sono allineati, cioè appartengono alla medesima retta proiettiva. Le operazioni di orientamento esterno hanno per oggetto la ricomposizione dei fasci proiettivi nello spazio oggetto, ma prima di questo, occorre fare alcune premesse sulle rototraslazioni con variazione di scala tra sistemi di riferimento. Difatti le basi della fotogrammetria analitica sono costituite dalle trasformazioni conformi nello spazio, che comprendono funzioni proiettive che si realizzano in traslazioni finite, in rotazioni, ed in variazioni di scala uniformi o meno. Si consideri, ad esempio, una semplice rotazione piana del sistema immagine (ξ,η), rispetto al sistema oggetto (X,Y).
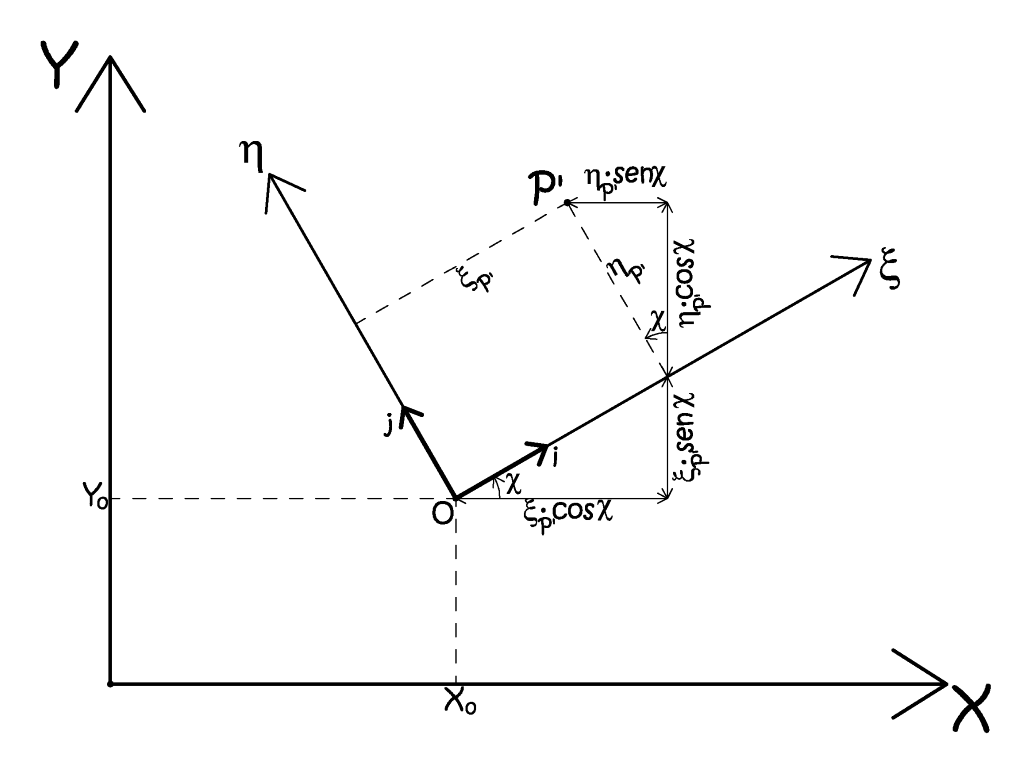
Fig. 2.33 – Rototraslazione del sistema di riferimento.
Osservando la figura 2.33 si ricava immediatamente che:

Passando alle matrici:
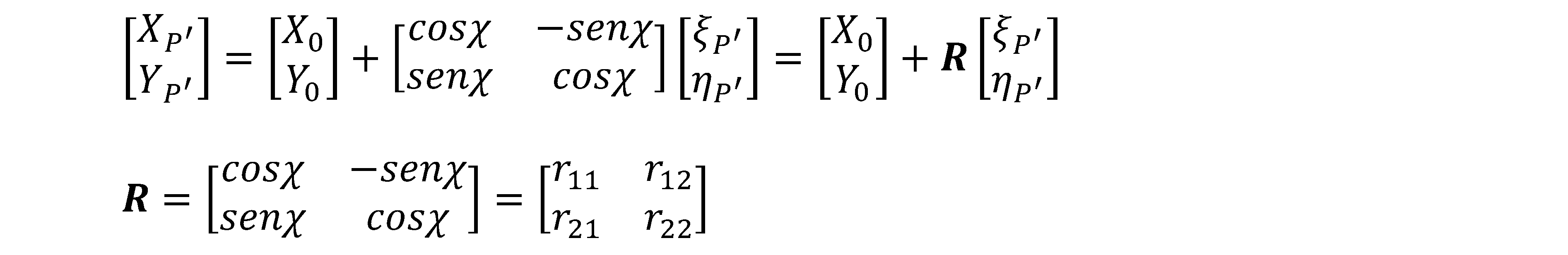
Riferendoci ai versori ie j, potremmo ottenere alcune proprietà notevoli delle matrici di rotazione in genere:

I versori i e j costituiscono una base ortonormale, difatti, per definizione, sono dei vettori di norma unitaria e ortogonali tra loro, ossia costituiscono una base ortogonale. Questa asserzione è fondata sull’esistenza delle condizioni di ortogonalità:
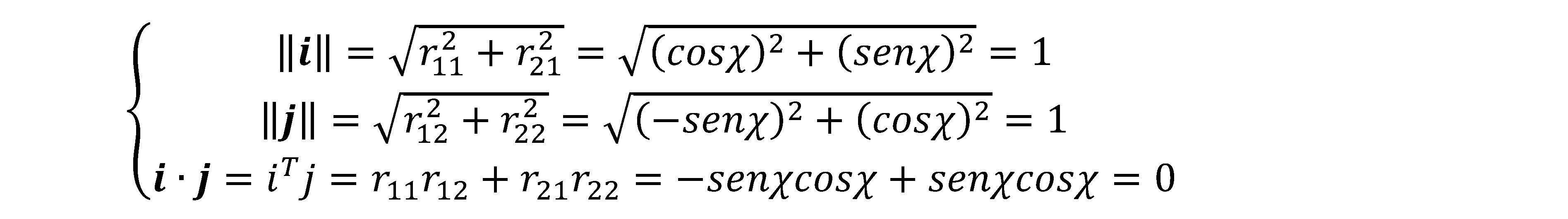
Se le colonne della nostra matrice di rotazione R configurano una base ortonormale, si può affermare che la sua inversa è la sua trasposta:
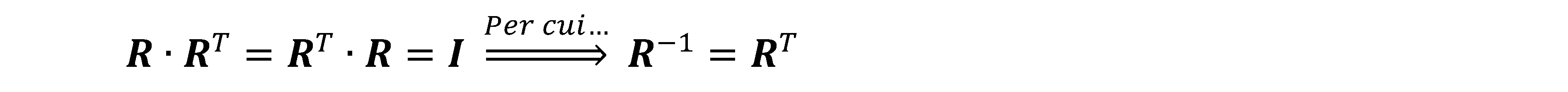
Il numero di parametri indipendenti di una matrice di dimensione N è (N(N-1))/2, quindi nel nostro particolare caso abbiamo un parametro indipendente, cioè l’angolo di rotazione χ. Per cui questa configura una trasformazione conforme senza variazione di scala. Vediamo ora di tradurre nello spazio a tre dimensioni, quanto visto nel piano, a tal proposito risulta conveniente considerare separatamente le tre rotazioni cardaniche indipendenti (Fig. 2.34).
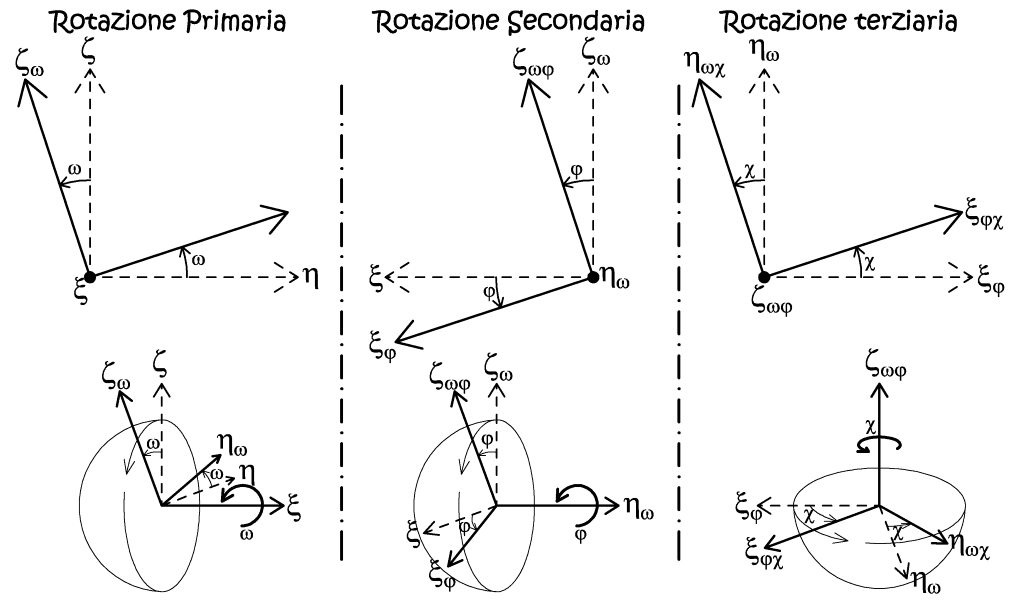
Fig. 2.34 – Sequenza delle tre rotazioni in un sistema cardanico.
Per ricavare la matrice rotazione R ωφχ in funzione delle tre rotazioni ω, φ, e χ, si scrivono le tre matrici che esprimono le tre rotazioni indipendenti della terna (ξ,η,ζ) e se ne esegue il prodotto.

Allo stesso modo di quanto visto per la matrice di rotazione, nel piano, anche quella nello spazio gode delle stesse condizioni di ortogonalità:

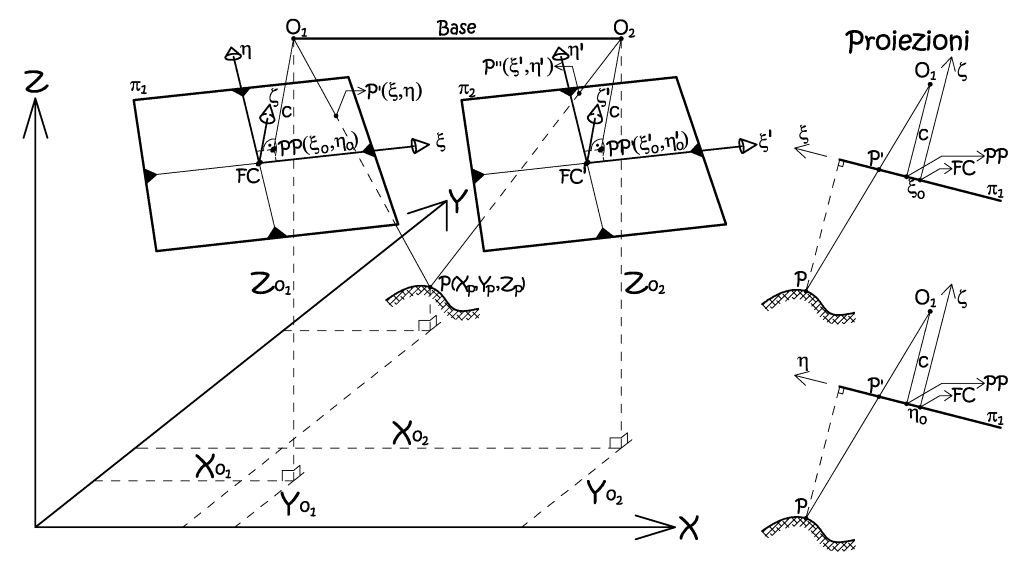
Fig. 2.35 – Rappresentazione di una doppia presa del medesimo punto oggetto P, a destra sono riportate le proiezioni secondo i due piani principali del sistema di riferimento interno (immagine).
Riprendendo la relazione precedente, ed osservando la Fig. 2.35, possiamo dedurre che qualsiasi trasformazione di rotazione nello spazio può essere espressa da una trasformazione conforme che, sistemando gli indici, può essere così espressa:

La relazione rappresenta la proiettività che governa il rapporto tra le coordinate di un medesimo punto, nei due sistemi di riferimento, diversamente ruotati nello spazio euclideo. Il fattore di scala λ, nel nostro particolare caso di studio, sarà sempre identicamente unitario, dato che i due sistemi di riferimento, rappresentano la realtà fattuale con i medesimi rapporti dimensionali. Esprimendo la matrice di rotazione in termini letterali, il tutto si traduce come segue:
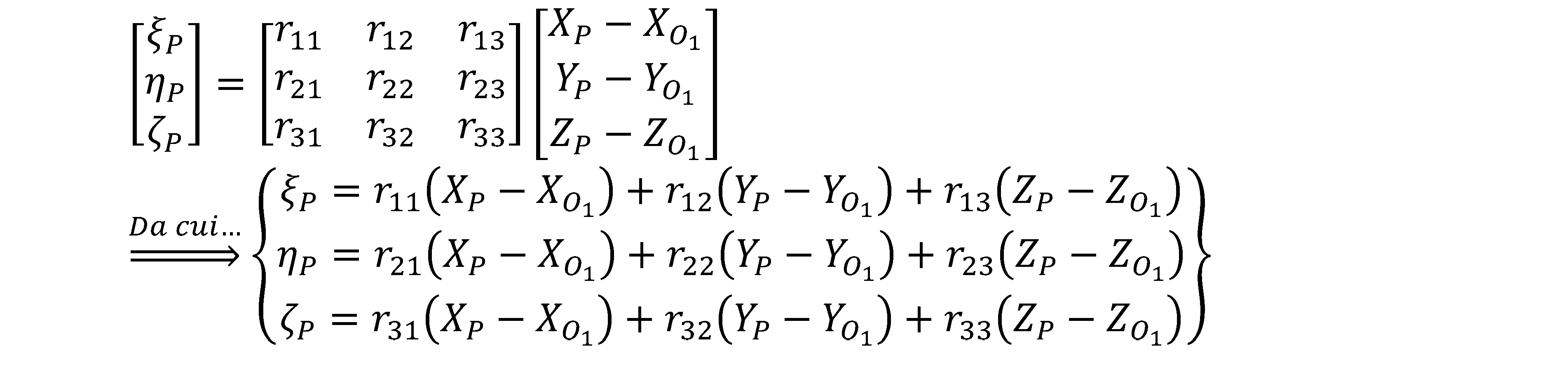
Il nostro fine è di trovare una relazione che leghi le coordinate del punto oggetto P, con il suo omologo P' sul piano della lastra π(1), per far ciò, e sempre in riferimento alla Fig. 2.35, ci ricaviamo delle semplici relazioni geometriche omotetiche (si trascurano gli infinitesimi di ordine superiore):
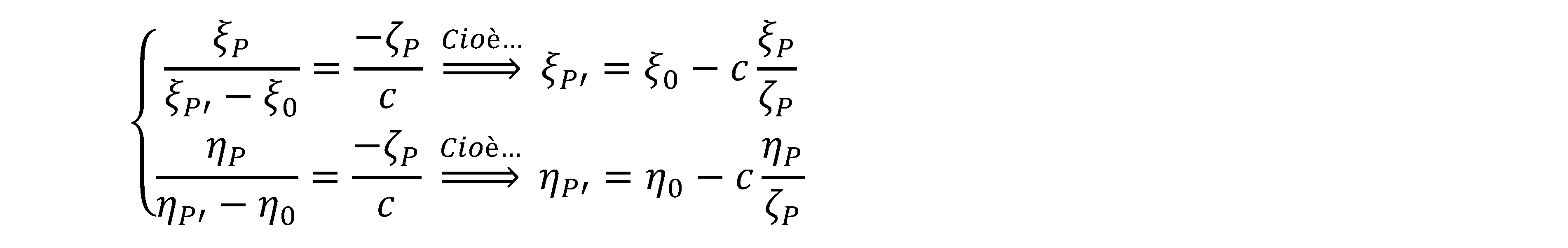
Operando le opportune sostituzioni e, generalizzando, otteniamo le relazioni che legano le coordinate dello spazio immagine (ξ,η) alle corrispettive coordinate oggetto (X,Y,Z):
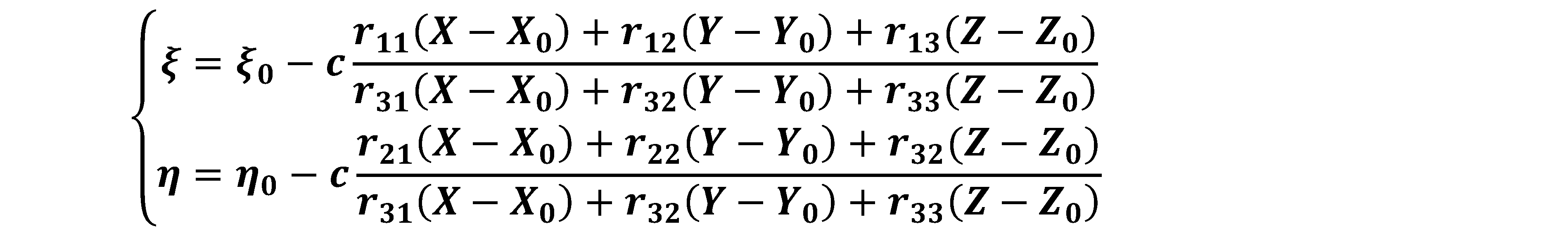
Queste relazioni prendono il nome di equazioni di collinearità, ed esse esprimono la condizione geometrica che il punto immagine, il punto oggetto e il punto di presa, appartengono alla medesima retta proiettiva. Queste equazioni dimostrano analiticamente quanto già affermato, e cioè che ad ogni punto oggetto corrisponde un solo punto immagine e che, invece a causa della presenza delle Z al secondo membro, per ogni punto immagine esistono infiniti punti oggetto. È quindi impossibile ricostruire la geometria spaziale di un oggetto a partire da un solo fotogramma. Ora, con semplici passaggi, possiamo ricavarci le inverse:
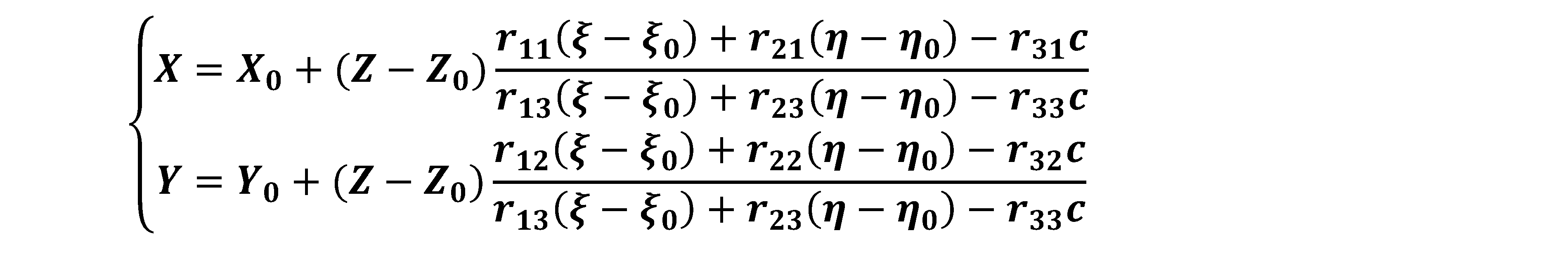
Con l’uso di due fotogrammi, per ogni punto collimato, possiamo scrivere quattro equazioni di collinearità: chiamando p il numero dei punti, abbiamo 4p equazioni di misura. Per ogni coppia di fotogrammi, cioè per ogni modello, abbiamo sempre dodici incognite: le coordinate dei due punti di presa e gli assetti angolari dei due fotogrammi; ed inoltre sono presenti le tre coordinate incognite di ogni punto collimato P(X P ,Y P ,Z P ), quindi il nostro problema potrebbe giungere a soluzione non appena:

Ma questa non è una condizione sufficiente, dato che, non si realizzano le necessarie condizioni di indipendenza tra le stesse equazioni, difatti scrivendo queste 4p equazioni, ed operando un’analisi di rango del sistema, si troverebbe sempre una deficienza dello stesso pari a 7, cioè un difetto di rango, che si può risolvere solo con la conoscenza diretta di coordinate di punti nello spazio oggetto. In particolare quello che manca è la conoscenza del datum, cioè i parametri della trasformazione conforme, che fissano la similitudine nello spazio, quindi le tre traslazioni, le tre rotazioni e il parametro di scala, che consentono di orientare la nostra configurazione spaziale delle stelle proiettive nello spazio oggetto. I parametri mancanti possono essere fissati con la conoscenza di due punti planimetrici, e tre punti di quota nota, non allineati. Ciò permette di risolvere ai minimi quadrati il sistema di equazioni di collinearità, previa sua linearizzazione, ricavando i dodici parametri di orientamento esterno, per altro la fase operativa assume lo stesso nome –orientamento esterno–. La procedura appena descritta va sotto il nome di orientamento simultaneo di due fotogrammi in una sola fase (Fig. 2.36). Tale metodo ha il vantaggio di essere molto preciso, in quanto permette di utilizzare un numero qualsivoglia di punti osservati.
RANGO DI UNA MATRICE.
Per rango si intende l’ordine
pdel minore con determinate non nullo, e tutti i minori con ordine
p+1, se esistono, hanno determinate nullo. Per minore di una matrice
Asi intende una sua sottomatrice quadrata, ottenuta intersecando opportunamente
nrighe ed
ncolonne di
A.
La nozione di rango ci permette di definire il teorema di Rouché-Capelli:
in tal caso, sia
Sun sistema lineare di
mequazioni in
nincognite, con matrice dei coefficienti
Ae matrice completa
A’. Allora:
a) S è compatibile se e solo se il rango di
Aè uguale al rango di
A’.
Supponiamo ora che S sia compatibile, e poniamo rk
A=rk
A’=r
b) Il sistema ammette una e una sola soluzione se e solo se r=n.
c) Il sistema ammette ∞^(n-r) soluzioni se e solo se r<n.
I metodi di orientamento esterno hanno anche risentito delle procedure operative utilizzate fino a pochi anni fa, sia nei restitutori analitici che analogici, come nell’orientamento simultaneo di due fotogrammi in due fasi successive (Fig. 2.36). Tale metodo si snoda attraverso due fasi ben distinte, nella prima, l’orientamento relativo, ove si orientano fra loro i due fotogrammi, fino all’intersezione dei raggi omologhi, con questa operazione viene creato il cosiddetto modello stereoscopico, avente come sistema di riferimento un sistema arbitrario (x,y,z). Nella fase successiva viene eseguito l’orientamento assoluto del modello, determinandone il fattore di scala, la posizione e l’assetto nello spazio, inteso come orientamento angolare, riferendolo quindi al sistema di coordinate oggetto (X,Y,Z). Riassumendo, il metodo prevede che si formi dapprima il modello stereoscopico, inteso come il luogo di intersezione di tutte le infinte coppie di raggi omologhi, e che quindi si roto-trasli questo corpo nello spazio in modo tale da riferirlo al sistema di riferimento esterno.
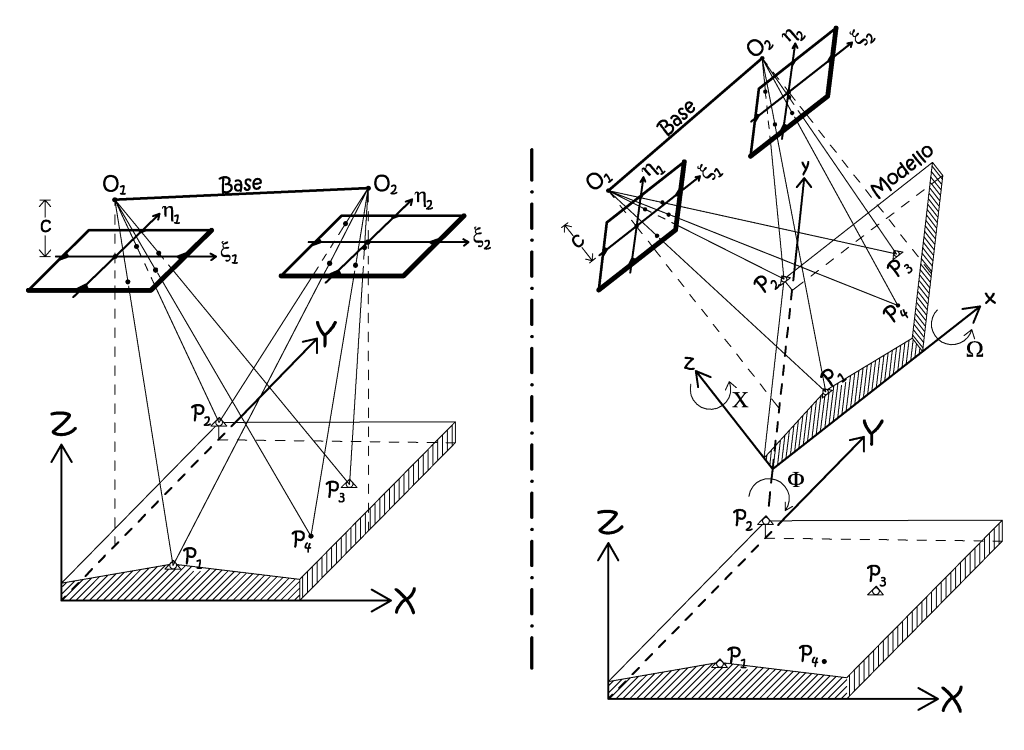
Fig. 2.36 – A sinistra l’orientamento simultaneo di una coppia di fotogrammi, in una sola fase, a destra l’orientamento della medesima coppia in due fasi successive, con la creazione intermedia del modello stereoscopico.
Esplicitare le coordinate modello era una necessità al tempo dei restitutori analitici ed analogici, oggi, nell’epoca digitale, rimane implicito nel processo di risoluzione, ed è fornito direttamente in output. Ad ogni modo, non vi sono ragioni per preferire questo sistema al metodo dell’orientamento in una sola fase, che è dunque da prediligere a meno di comprovati motivi di ordine pratico.
Il metodo della triangolazione aerea.
I metodi descritti in precedenza sono da intendersi come accenni storici, oggi, le consolidate procedure digitali di restituzione permettono una flessibilità nettamente superiore. In primis, va considerato che le vecchie tecniche non consentivano di concatenare fra loro non più di due fotogrammi alla volta, con la creazione dei rispettivi modelli stereoscopici. Ma nella pratica spesso i fotogrammi da orientare e restituire possono essere decine, e difatti definiremmo blocco aereofotogrammetrico l’insieme delle strisciate, e dei fotogrammi componenti le stesse, oggetto di orientamento e restituzione. Quindi nell’ambito della triangolazione aerea si parla non di coppie di fotogrammi, ma di blocchi di fotogrammi stereoscopici. Questo metodo libera la fotogrammetria dalla necessità di disporre di almeno tre punti d’appoggio fotografici per ogni modello, le cui coordinate dovevano essere rilevate sul terreno. Al contrario nella triangolazione aerea vengono molto utilizzati i punti legame (Tie points), questi sono di coordinate oggetto incognite, ma sono punti in comune a due o più fotogrammi. Due sono le tecniche possibili per il calcolo di una triangolazione fotogrammetrica, che costituiscono la generalizzazione dei due metodi di orientamento di coppie fotogrammetriche visti in precedenza. Possiamo avere la compensazione di un blocco col metodo delle stelle proiettive (Bundle Adjustment), ove l’entità elementare oggetto di orientamento è il singolo fotogramma, oppure possiamo usare il metodo a modelli indipendenti, in questo caso l’entità elementare è costituita dai singoli modelli, ottenuti dopo aver eseguito l’orientamento relativo dei fotogrammi del blocco.
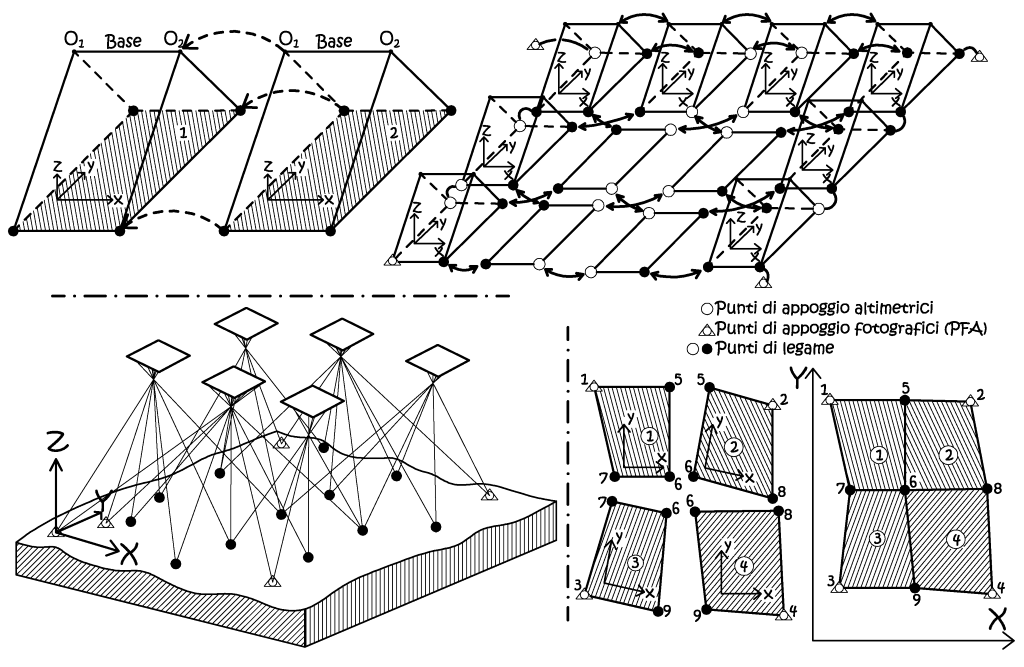
Fig. 2.37 – Metodo della triangolazione aerea nei suoi due modi di orientamento: il metodo a modelli indipendenti, ed in basso a sinistra, il metodo delle stelle proiettive (Bundle Adjustement).
La compensazione a modelli indipendenti parte dalle coordinate modello, ottenute dopo che si è effettuato l'orientamento relativo analitico e si è formato ciascun modello. Nel corso della compensazione del blocco, ogni modello verrà connesso agli altri in un unico blocco e, contemporaneamente, trasformato nel sistema di riferimento terreno. Oltre alle coordinate modello dei punti di appoggio e di legame, vengono ad essere considerate anche le coordinate dei centri di presa, ricavate dall’orientamento relativo analitico e dalla formazione del modello. Ogni modello quindi verrà ruotato, traslato e dimensionato con un opportuno fattore di scala, singolarmente, in maniera tale per cui i vari punti di legame risultino il più possibile coincidenti e che gli scarti residui sui vari punti di appoggio siano minimi. In altri termini viene utilizzata la classica trasformazione conforme a sette parametri, vista in precedenza. Questa tecnica non è molto utilizzata a meno che non si voglia separare l’aspetto altimetrico da quello planimetrico, operando una compensazione separata delle due entità. Infatti nella compensazione tridimensionale del blocco a modelli indipendenti, la precisione planimetrica risultante non è influenzata dalla precisione delle quote modello, perciò le precisioni planimetrica e altimetrica si possono trattare separatamente.
Nel metodo delle stelle proiettive, l’entità elementare che viene roto-traslata nello spazio è il singolo fotogramma (Fig. 2.37), in modo che i raggi si intersechino al meglio in corrispondenza dei punti di legame, e passino il più possibile per i punti di appoggio. Similmente a quanto avviene “nell’orientamento simultaneo di due fotogrammi in una sola fase”, vengono ad essere calcolate direttamente le relazioni intercorrenti tra coordinate oggetto ed immagine, senza l’introduzione delle coordinate modello quale passaggio intermedio. Il sistema di equazioni alle osservazioni presenta, come incognite, i 6 parametri di orientamento esterno per ogni fotogramma e le tre coordinate oggetto di ogni punto di legame. Il sistema, ridondante, si risolve con il metodo della compensazione ai minimi quadrati che fornisce le correzioni da apportare ai valori approssimati delle incognite e i valori dei residui sulle osservazioni. A tale scopo le equazioni devono essere linearizzate. Oggi grazie all’uso delle stazioni fotogrammetriche digitali è il metodo più utilizzato, dato che tali soluzioni consentono, in breve tempo, di risolvere ampi sistemi di equazioni non lineari. La compensazione è tridimensionale, quindi il problema non può essere separato nella parte altimetria e in quella planimetrica, ma questo consente di raggiungere la maggiori precisioni possibili, dato che si basa sulla relazione diretta fra coordinate immagine e quelle oggetto, senza alcun passaggio intermedio.
La precisione della triangolazione aerea.
Le considerazioni qui riportate valgono qualunque sia la compensazione utilizzata (a modelli indipendenti o a stelle proiettive). Negli anni passati sono stati svolti degli studi sperimentali che puntavano a definire le precisioni ottenibili, andando a variare la distribuzione dei punti d’appoggio presenti all’interno del blocco aereofotogrammetrico. In modo particolare si è notato che utilizzando uno schema d’appoggio molto semplice, cioè quattro PFA (Punti Fotografici d’Appoggio) nei quattro vertici del blocco, si è notato che la precisione degrada fortemente al cresce delle dimensioni del blocco, e lo scarto quadratico medio è massimo nelle zone di mezzeria dei lati del blocco.
Da queste semplici deduzioni, appare del tutto evidente che questi effetti deleteri sulla precisione possono essere attenuati andando a predisporre una serie fitta di PFA lungo i bordi del blocco, in questo caso si può dimostrare che la precisione diviene quasi indipendente dalle dimensioni del blocco, ed è simile a quella del singolo modello, ulteriori punti all’interno del blocco non portano ad aumenti apprezzabili della precisione finale. Questi risultati sono stati ottenuti, in tempi diversi, da Ackermann (1968), Ebner (1972) e Meissl (1972), relativamente alle diverse disposizioni dei PFA, come si può vedere in figura.
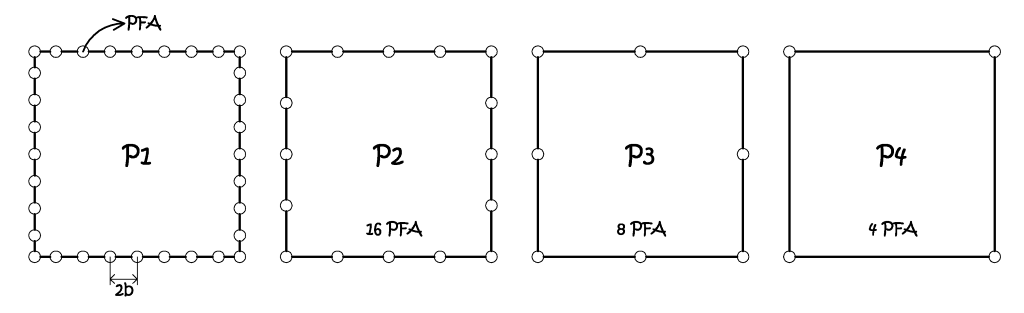
Fig. 2.38 – Quattro diverse configurazioni dei PFA.
Nella Fig. 2.38 abbiamo configurazioni diverse dei PFA, nel primo caso il loro numero è indefinito, ma la loro distanza reciproca è pari a due basi, quindi il loro numero aumenta con la dimensione del blocco, mentre nei restanti tre casi la dimensione del blocco è la medesima, a diminuire sono i punti d’appoggio. Gli autori citati, riportano le seguenti relazioni empiriche per la valutazione della precisione, nei quattro casi considerati:
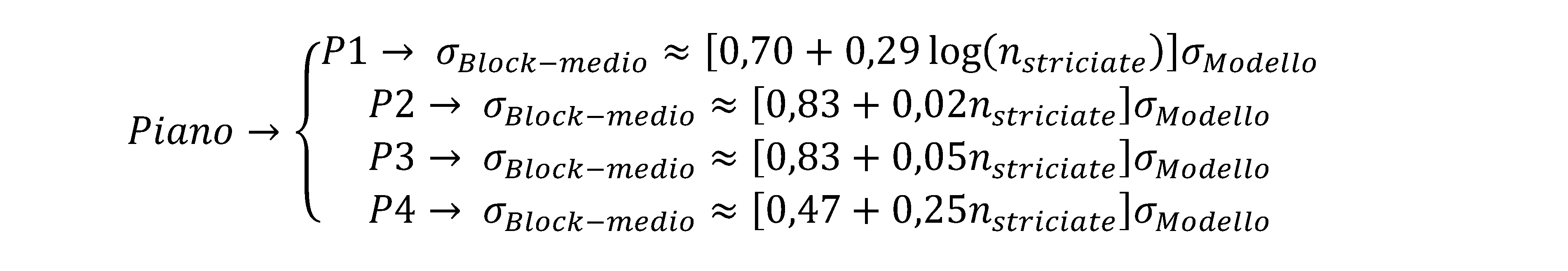
Queste regole sono applicabili anche al caso di blocchi rettangolari, ma non possono essere usate nel caso limite della singola strisciata, ove viene richiesta una trattazione diversa. Si noti che nel primo caso [P1], quello più rilevante, si ottiene una precisone di blocco molto simile a quella del singolo modello, tale asserto continua ad essere vero anche con blocchi dal bordo non regolare. In analogia con la precisione planimetrica, lo stesso può essere fatto per la precisione in quota, difatti essa dipende dal numero di modelli i compresi tra due serie di punti d’appoggio altimetrici, disposti lungo la perpendicolare all’asse delle strisciate (Fig. 2.39). In particolare, per aumentare la precisione lungo i bordi superiore ed inferiore del blocco, è consigliato introdurre dei punti d’appoggio altimetrici a i⁄2 .
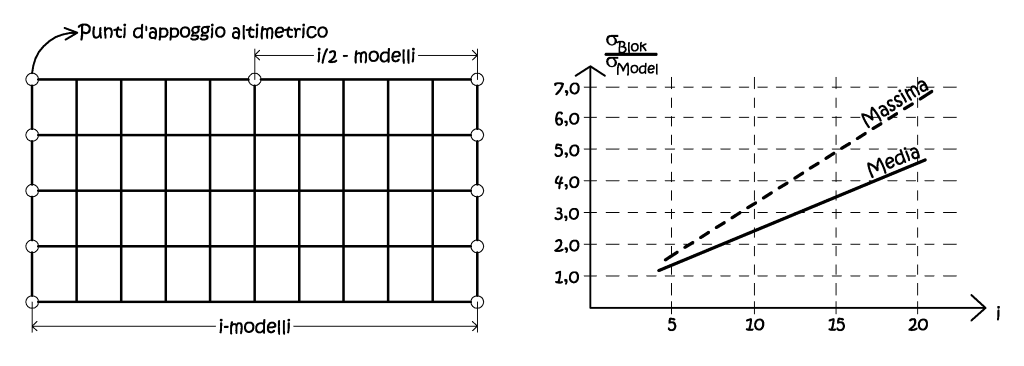
Fig. 2.39 – A sinistra l’ideale distribuzione dei punti di appoggio in altimetria, a destra, il rapporto tra la precisione del blocco e quella del singolo modello, medio e massimo.
In Fig. 2.39 è mostrata la relazione che intercorre tra la precisione, o meglio, tra lo scarto quadratico medio dell’intero blocco e del singolo modello, sia medio che massimo, nel punto più sfavorevole. Le espressioni empiriche sono le seguenti:
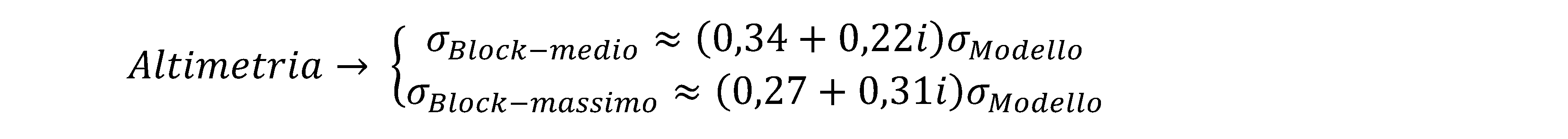
Dal confronto di queste relazioni con le precedenti, soprattutto nel caso di appoggio fitto (P1), si nota come la precisione ottenibile in quota sia meno favorevole, ed è questa una caratteristica peculiare della restituzione fotogrammetrica. D’altronde la configurazione geometrica spaziale del blocco fotogrammetrico è a prevalente sviluppo piano, ed è proprio lungo tale dimensione che esso offre una maggiore “rigidezza all’errore”, a vantaggio delle precisioni ottenibili. Tornado all’analisi delle precisioni in quota, se si vuole limitarne il decadimento rispetto alla precisione del singolo modello, sarebbe auspicabile limitare a tre modelli, l’interasse esistente fra le linee dei punti d’appoggio. Ma questo rederebbe il rilievo a terra troppo oneroso, quindi un buon compromesso tra precisione ed economicità, potrebbe prevedere almeno quattro modelli d’intervallo.
Si è fatto cenno al fatto che il caso di una singola strisciata richieda una trattazione a parte, ebbene, studi teorici e sperimentali hanno spesso condotto a risultati discordanti, è per questo che in questa sede ci si limiti a riportare un grafico di facile comprensione. La precisione dei punti ricavati dipende dal numero i di modelli compresi tra punti d’appoggio successivi; come al solito lo scarto quadratico medio è espresso nel suo valore medio, e in quello massimo, nell’ambito planimetrico e in quello altimetrico (Fig. 2.40).
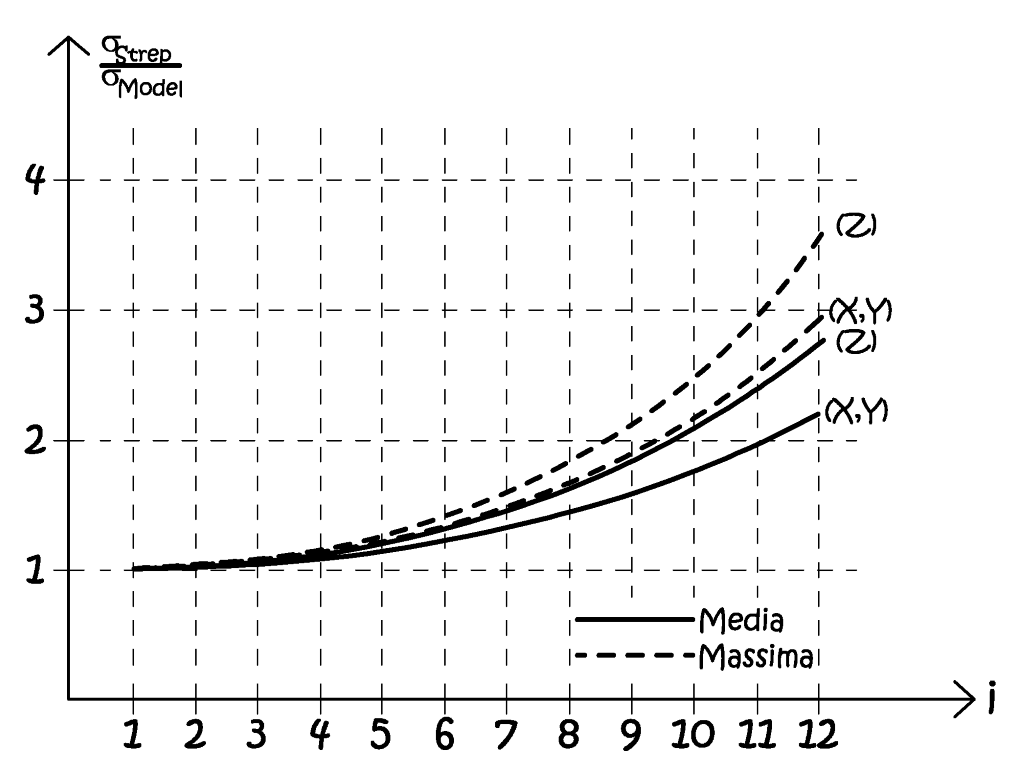
Fig. 2.40 – Precisione della triangolazione aerea nelle singole strisciate, in rapporto con la precisione del singolo modello.
Le relazioni fin qui riportate si basano su osservazioni di natura sperimentale, e come tali devono essere considerate, dato che, nella realtà operativa le condizioni al contorno possono essere diverse. Da queste considerazioni, ma anche da altre valutazioni di natura operativa, in generale, i punti d’appoggio fotografici (PFA) plano altimetrici dovranno essere posizionati seguendo questi criteri.
• Lungo le strisciate esterne, nel senso del volo, ogni due o tre modelli.
• All’interno del blocco, nelle aree di sovrapposizione fra strisciate
adiacenti, ad un interasse variabile da quattro a cinque modelli.
• Ai vertici esterni del blocco fotogrammetrico, almeno due punti PFA
a breve distanza l’uno dall’altro.